多重分形与地质统计学方法在粤北刘家山地区矿

　　在矿产勘查中，场的局部变化性和空间结构信息对识别异常是非常重要的。因为这种局部的变化性和空间结构通常反映了一定的地质控制因素。而通常的数据插值方法如反距离滑动平均法、克里格法及样条函数法等常常会对原始数值造成一定的光滑，因为使用这些方法的目的通常是为了体现某种趋势，它们并不突出场值的局部变化和特征。而多重分形方法不仅考虑了场值的空间相关和变化性，而且能够有效地度量场的局部奇异性，它对突出异常的局部变化特征和识别与矿有关的异常具有较好的应用效果。文中将该方法用于刘家山地区地球化学数据处理。同时为进一步研究奇异性与异常的关系，还将采用一种由多重分形理论所导出的场的滤波和分解方法——分形滤波技术（s-A法）分解奇异性与异常地段的关系。该方法已成功应用于地球化学异常分解中。

　　1研究区地质背景

　　刘家山铅锌矿是2002年5月通过矿点调查开始发现的。刘家山铅锌矿区①位于广东省始兴县城162°方向，平距约24km处，面积约10km2。铅锌矿主要赋存于奥啕系龙头寨群下亚群中部及底部，该区处于粤北坳陷与武夷隆起过渡地带的隆起侧，贵东岩体北部，属瑶岭褶皱带，北东向、北西向、东西向构造交汇区。该区总的属中低山地区，水系非常发育，地形切割强烈，常形成悬崖峭壁等险峻地形。本区矿产主要有锌、铅、铜、银、钨等。北面有石人嶂、梅子窝、师姑山等中小型钨矿床；南西面有新凉亭、寨背坑等小型铜铅锌多金属矿床。2003年广东省地质调查院在该区开展1:5万水系沉积物测量工作时，发现了铅锌富矿体。

　　2地质统计学与多重分形法对比分析

　　对于以矿产勘查为目的的数据处理和异常分析，保持和突出与矿有关的局部异常是数据处理和分析的关键。变异函数通常用于描述场的局部变异性和进行结构分析，它可以突出一定尺度的局部变化性，但是忽视了场的局部奇异性[]。对于岩石中元素含量来说，局部奇异性反映的是元素在地质过程中的富集和贫化规律。而多重分形插值方法[]不仅可度量这种局部奇异性，同时还考虑了局部空间相关性，它能够保持和突出场值的局部空间结构和奇异性信息。

　　2.1地质统计学法

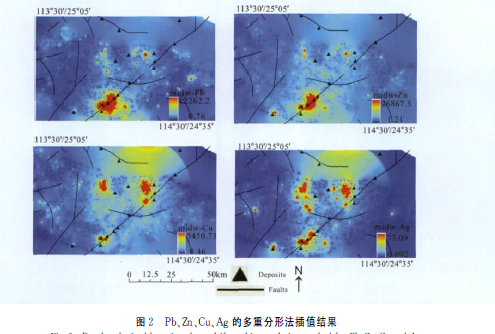
　　地质统计学方法将空间自相关性和变异性引入插值估计中，它可以反映一定的空间结构和变异信息。地质统计学方法在地球化学异常的分析和识别中起到了积极作用，它是在满足内蕴假设的前提条件下采用半变异函数来度量：

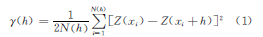
　　式中：Z(:r)为区域化随机变量；h为两样本点空间分隔距离；Z(:r,)为Z(x)在空间点处的样本值；Z(xt+h)是Z(x)在xt处距离偏离h的样本值[<=1，2，-"，N(h)];N(h)是分隔距离为h时的样本点对总数。该半变异函数可用于多方向多尺度结构分析[8]。克里格法是基于半变异函数的一种空间插值方法，它实质上是一种滑动加权平均方法[]。它是以空间变异性为原则进行加权平均，所以不可避免对数据造成平滑。这种方法往往能够有效地计算储量等参数估计值，但是对于异常分析来说，其局部变化信息的抑制可能会造成有用信息的丢失。

　　2.2多重分形法

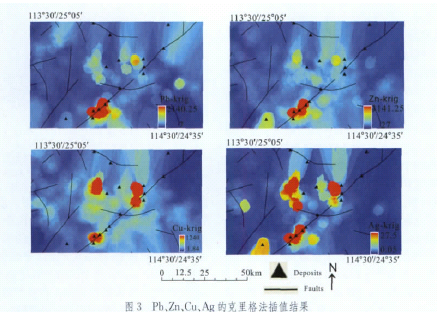
　　多重分形法由Cheng[7]提出。他提出的这种方法同时考虑了局部空间相关性和奇异性，其主要作用是保持和突出场值的局部空间结构和奇异性信息。Cheng[11]»滑动平均关系表示成：

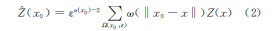
　　式中：fK：x，e)代表以x为中心半径为e的小滑动窗口-，CO(||xfxII)为对在0(2。，)中与点x0距离IIx0—xII的任意点x的加权函数；a()为奇异性指数，当x为0时a(r)等于a(：x)。

　　当局部场具有奇异性且处于含量富集区域时«(：x)<2，利用上式计算的结果将大于普通的加权平均结果；当局部场处于贫化区域时《(：x)>2，利用上式计算的结果将小于普通的加权平均结果；当局部场为背景场或非奇异场时a(x>)=2。可见，普通的加权平均方法是多重分形法的特殊情况。前人采用Q-Q图和聚类分析等统计方法证实了传统统计法不适合具有奇异性的地球化学数据，而多重分形法不仅能用于表示地球化学数据的统计分布，更能刻画场的奇异性。

　　2.3实例分析

　　文中以刘家山1:5万水系沉积物样品（样品取样位置见图1，通过软件ArcGIS导出）中Pb、Zn、Cu、Ag为例进行说明。首先采用多重分形法对样品中这4种元素的奇异性分布进行研究和异常识别，图2是多重分形插值的结果。通过成秋明团队开发的GeoDAS软件包计算后导入ArcGIS中成图(经多次实验对比分析，最终参数设置为：窗口边长为12km,滞后距取1km)。研究表明，刘家山地区多种元素（其中包括Pb、Zn、Cu、Ag等）的分布都具有多重分形特征。为比较多重分形方法与克里格方法结果，将克里格方法也用于1573个水系沉积物Pb、Zn、Cu、Ag元素含量数据。图3是普通克里格插值的结果，通过ArcGIS软件导出（所采用的半变异函数模型为球状模型，搜寻半径为12km)。从插值结果图可看出，Pb、Zn异常区主要分布在研究区的西南段，Cu、Ag异常区分布在中部和西南段。这一结果与刘家山矿区铅锌矿普查报告①相吻合，后期开采工作中在该地段发现铅锌银矿。

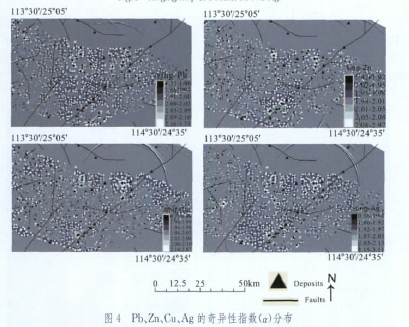
　　为了应用多重分形方法，需要先计算局部奇异性指数。成秋明[4研究发现，奇异性指数与热液成矿的成矿系数是相关的。鉴于奇异性指数这样的特性，对该区成矿元素奇异性指数作进一步研究是有必要的，且该区矿床为层间破碎带型热液充填交代矿床，其奇异性指数对于矿化异常的增强和识别是非常重要的。从地球化学数据的角度来研究奇异性指数，利用地球化学数据对奇异性进行分析可以得知成矿元素密度的奇异分布模式，从而为不同的地质异常如矿化作用、局部地质构造等的解释提供参考信息。选取刘家山地区4种成矿元素Pb、Zn、Cu和Ag，对其奇异性指数作研究见图4(图2、中有些圆形明亮区或圆弧状高值区，它们超出了数据点的范围，属于软件产生的伪影，实际研究中可不予考虑）。图4显示了奇异性指数的分布与控矿地质条件以及矿床分布的空间关系，对比奇异性指数图和各插值结果图可以看出，《(：r)<2的区域成矿元素的密度显示升高，与断层走向东南方向走向一致，与异常区域相对应，这说明该区域与矿化富集有关，而《(：r)>2的区域显示元素含量亏损。这与已知报告中的结果吻合。

　　为进一步分析多重分形法与普通克里格法在该区的适应性，研究其比值结果，图5为图2与图3的比值，从比值图中可以明显看出，比值高的地段为那些具有奇异性的地段，高比值区域与高异常区相吻合，这说明了多重分形法较克里格法能够较好的增强矿化富集地段的信息，通常元素局部富集地段分布局限，且为线性规律，而这些与矿有关的空间信息在克里格图上是没有明显反映的。

　　3分形滤波技术(S-A法）

　　为进一步研究奇异性与异常的关系，采用S-A法分解异常与背景。该方法已在GeoDAS软件中实现。

　　3.1 S-A法原理

　　S-A是空间分析和频谱分析的集成，利用频域中明显的广义自相似性，并采用滤波的方法选取频率信息重新恢复空间模式将异常从背景中分离出来。能谱密度S与能谱密度大于S的波数集合的面积A之间的关系为

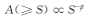
　　上式取对数并用最小二乘法对IgA-IgS进行分段拟合可求出对应于不同能谱密度范围的幂指数根据能谱密度设计滤波器滤波，从而达到对场分离的目的。

　　2. 2应用S-A法分离异常和背景

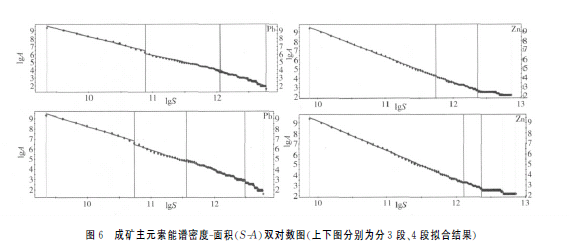
　　应用S-A法对Pb、Zn、Cu、Ag元素含量多重分形图进行处理。此处只给出成矿主元素Pb、Zn的结果(图6)。

　　通常S-A双对数图分3段拟合直线（基于最小二乘法原理）。文中针对该研究区实际情况加以分析，基于最小二乘法原理来确定分界点，基本思想是计算各区间剩余平方和（剩余平方和为拟合数据与原始数据差值的平方和，该值越小，拟合精度越高）也即拟合误差，分为3段后Pb能谱密度3个区间段分别为11497〜53457、53457〜171007和171007〜351896，3条直线段的斜率分别为一2.03、一1.82和一2.75，截距分别为28.59,25.98和37.09。为检验各区间段回归方程的显著性，对各个方程进行误差检验，计算得到各段拟合误差分别为0.01、0.003和0.01。同样使用最小二乘法分4段拟合时，各区间段为11497〜46203,46203〜地学前缘，012，19(4)104783,104783〜265844,265844〜351896，计算斜率分别为-1.94、一2.12、一2.28和—3.67，截距分别为27.68,29.31,31.37和48.68。各段拟合结果误差分别为0.006、.006,0.003和0.008。对比两种情况的误差结果可知4段拟合精度较3段高，故采用4段法进行异常背景分离。以265844为阀值定义两个滤波器：异常滤波器S<265844;背景滤波器S>265844。

　　Zn能谱密度使用最小二乘法分3段确定的各区间段为19428〜126269、126269〜234619和234619〜383884，各段斜率分别为一2.83、一2.38和-1.11，截距分别为37.51,32.24和16.51。各段拟合误差分别为0.003、.002和0.006。使用最小二乘法分4段拟合时各区间段为19428〜181338,181338〜233094,233094〜317734和317734〜383884。4条直线段斜率分别为+2.82、一2.44、一0.43和一0.57，截距分别为37.38、32.88、.98和9.59。各段拟合结果误差分别为0.002、.001、.002和0.002。同样对比分析可知4段拟合精度较3段高，故采用4段法进行异常背景分离。以233094为阀值定义两个滤波器：异常滤波器S<233094；背景滤波器S>233094。从S—图（图6)中可以看出，该图总是显示下降趋势，因为随着能谱值的增加，高能谱值区域的面积值总是减少的（对该区域其他元素进行研究也得到同样的结果）。

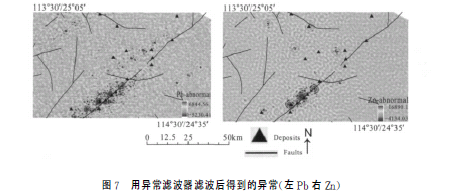
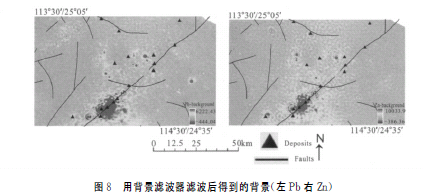
　　异常滤波器所得的结果（图7)主要反映原始元素含量的高频成分，它包括元素的局部异常含量和与插值相关的随机噪声，局部异常沿西南方向分布且与西南段断层走向一致，可根据图7中的具有明显方向性的局部异常分布判别Pb、Zn矿床（点）的分布位置；背景滤波器所得的结果图是元素含量的背景成分（图8)。从图8中可以得知，较高的背景变化可能代表了Pb、Zn成矿的有利地质背景，高背景的地区可能指示了Pb、Zn矿床勘查的有利区域。

　　S-A法的独特性在于它是采用不规则的或是分形滤波器来反映空间能谱的自相似性，被分解的场必将保持一定的空间异向性。研究表明，使用S-A法分解的局部异常通常与矿化蚀变有关。

　　4讨论

　　相对于传统统计方法，多重分形方法更能突出局部异常的奇异性规律，对于地球化学数据而言，局部奇异性可以反映矿化元素的富集或贫化规律，多重分形方法将空间相关性和局部奇异性结合起来，突出了局部的矿化信息，对地质工作者找矿工作起到了一定的指示作用。因为研究区属于低山地区，植被发育，远离村庄，矿床开采在地下深部进行，对地表土地资源占用不多，对环境造成的影响较小；而观测数据是水系沉积物地球化学数据，地形因素和水流对水系沉积物异常空间位置可能造成一定的影响，水系沉积物异常和真正的异常源之间往往沿水流方向和陡坡方向存在漂移。而且还可能受到异常源埋藏深度的影响，而奇异性方法所得的分析结果在一定程度上消除了隐伏源深度的影响，它所圈定的局部异常已在刘家山研究区较好地对应了已发现的铅锌矿床的分布，为进一步开展铅锌矿勘查提供了重要耙区。

　　通过S-A法对异常与奇异性区的进一步研究发现由S-A法分解得到的异常区与奇异性区一致，并且得出由S-A法分解的异常具有局部奇异性的结论。从本文分析中得知，粤北刘家山地区内具有明显奇异性的地区也即元素富集区域是铅锌矿异常区域，它们与铅锌矿成矿作用和已知矿床的赋存密切相关，异常区大多处于西南段，在该区已探明部分铅锌矿床，需作更为深入的调查研究，后期的详查工作可着重从该方位入手，这一指示也为该地区元素的成矿潜力评价提供了重要的线索。后期工作时于外围始兴县深渡水铅锌矿点发现的铅锌矿化钾长岩脉，铅锌银等有用组分已高度富集，验证了采用多重分形方法圈出的异常的准确性，可作为该区寻找多金属矿床的找矿线索；同时发现钾长岩具有一定规模，可以作进一步调查。

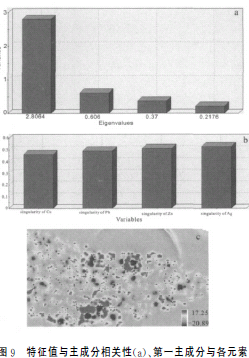
　　为了进一步描述异常区与各元素的相关性，采用主成分分析法来分析奇异性值，同样选用Pb、Zn、Cu和Ag，计算得出特征值见图9a，它反映了每个因子的重要程度，从图中观察得知第一个因子大约占总数的70%，第一因子对各个元素的贡献见图9b。图9c显示了第一主成分在各样点上的因子得分的结果。这些结果显示局部异常范围大多处于西南段，也即有少数已知矿点的区域。北东段与西南段恰好成对角状范围内也发现较大面积异常区，这与前面用S-A法分析得到的异常方位相吻合，且该处异常形态更为明显。然而北东段方向目前还没有发现任何矿点信息，下一步工作可从该方位入手寻找新矿床。