基于改进DS理论的双重模糊信息安全评估
引言
2015年度3.15晚会,央视曝光了包括众多国家通信部门在内的非法信息侵权,信息安全再度引起热议,国家工作报告中,网络信息安全也被加以重视,逐步做好立法相关工作,信息安全的产业需求或迎来扩张。各种产业的网络化和信息化使得网络信息安全直接关系到各个领域的安危,因此必须做好对信息安全的评估工作,以避免或减少信息安全风险对各相关产业造成的损失。
针对信息安全评估问题,国内外不少文献都对评估方法进行了详细论述。文献对专家打分进行预处理,根据评价指标的权重大小,将分数转化为相对权重比值,再运用模糊聚类法剔除离散程度较大的差异分数,减少评判者的主观差异性,但是这种简单剔除就使本项决策丧失作用,不能得到合理运用,使其发挥作用;文献将基于Markov链的评估模型引人到信息系统安全风险评估中,完善了基于模型的信息安全风险评估方法,基于Markov链模型也考虑了不同的危害等级以及组件之间关联,但是它只是按照任务的执行顺序计算风险值,而忽略了所有组件问题组成了整个评估的整体,因而没有从全局上进行评估;文献引人贝叶斯网络推理算法,并结合专家知识给出贝叶斯网络下的推理规则条件概率矩阵,构建了信息安全风险评估模型,这种基于诊断的推理过程使评估结果变得客观;文利用粗糙集理论的属性约简和属性值约简对评估指标进行优化,获得最简规则。
根据决策表中的属性重要性确定证据在粗糙D-S理论合成公式中的权值,以决策表为依据获取基本概率分配,建立系统安全评估模型;另外,还有基于支持向量机的解决凸优化问题的思路,提供了一个基于最优分类面的解决办法,这样容易把复杂问题简单化,忽略掉一些重要信息;基于决策树[6]的算法分类速度快,容易形成分类规则,从树根往下每一个分裂条件都可以形成一个确定分类谓词,对于绝对正确的信息来源分类准确性高,但对于专家评估,不是所有的原始数据都正确可靠;基于BP神经网络的评估算法很好地利用了智能的正向和反向传输验证网络构建威胁与后果等级的非线性映射关系;变权证据合成、支持向量域、风险矩阵'多层次模糊综合评判[11]等的信息安全评估方法也都是在一次模糊的基础上进行的;文献利用DS理论处理评估过程中专家认知判断信息的不确定性问题;文献[13]将语言评价转化为定量的模糊评价,利用三角模糊数来建立信息安全风险的可能性矩阵和损失矩阵,然后通过对专家意见的集结,得到信息安全风险矩阵。很多文献只关注了专家的评价态度,以及不同专家间的偏差,但是忽略了专家做决定的前提条件,也就是信息安全系统的表现,这个前提条件会导致专家个人本身的评价偏差,或是无法做出决定系统到底处于那个级别,而对这样的结果进行整合重组和处理是没有太大意义的。本文提出一种先对专家本身观点进行整合,然后再对专家间不同观点进行集结的方法,从而避免了或减小了因为专家本身的犹豫而造成的结果偏差,双重评估使结果更加客观,为管理者提供了更有效的管理依据。
2 DS证据推理
对于解决不确定性问题,Dempster-Shafer证据推理已在很多领域发挥作用,如目标识别、决策分析、数字图像处理、网络人侵检测等,它是Dempster[14]在1967年提出,后经Shafer改进扩充的。不确定性的描述可以用概率,但是DS推理方法采用的是区别于概率的信任函数。DS理论是概率的一种不完备延伸,它是基于不精确概率的一种表现形式,其取值为一概率区间,比单一取值的概率更能表达不确定性,所以这里信息安全系统选择它作为情况不确定性的描述方法。
2.1 DS相关定义
定义1(识别框架)问题的所有可能取值组成的集合,且集合内所有元素互不相容一般记为©。
定义2(基本概率赋值函数m(A))设©为一识别框架,则基本概率赋值函数m(A):20^[0,1]满足如下条件:
(1) m(小)=0;Zm(A)=1 (2) A=®。
定义3(信任函数)设©为一识别框架,m:20^[0,1]是©上的基本概率赋值,信任函数Bel满足下列条件:
Bel:20—[0,1],Bel(A):Bel(A)=Zm(B)B=A,(VA®)。
定义4(焦元)若A为识别框架©的一子集,且有m(A)>0,则称A为信任函数Bel的焦元,所有焦元的并称为核。
定义5(似真函数)设©为一识别框架,定义似真函数Pl:20^[0,1]为:
Pl(A)=1-Bel(A)=Zm(B)。BnA辞
定义6(Dempster组合规则)设Bel!和Bel2
是同一识别框架©上的两个信任函数,瓜丨和m2分别是其对应的基本概率赋值,焦元分别为4,…,Ak和Bi,…,Br,设:
K=Zm1(Ai)*m2(Bj)则 'Zm1(A,)、(Bj) m(C)=\An¥C^ ,VCe0,C其命.1-K ,0,C=^.(1)
说明:,若K—1,则m确定一个基本概率赋值;若K=1,则认为m1和m2矛盾,不能对基本概率赋值进行组合。当有多个证据时,可采用此组合规则对证据进行两两组合综合。
2.2改进DS理论
在证据冲突较小,即证据都倾向于一种或多种因素,而不是出现两种极端偏差时,DS证据理论组合规则能够向确定性较高的因素靠拢,但是,在证据冲突较大甚至完全对立时,由于DS证据理论将冲突全部丢弃,没有了融合效果,结论则常常与事实不符。比如,在识别框架©={Y1,Y2,Y3}下,有两条证据:m1(Y1)=0.9,m1(Y2)=0.1,m〗(Y3)=0;m2(Y1)=0,m2(Y2)=0.1,m2(Y3)=0.9,
按照DS证据组合规则得,
K=m1(Y1)*[m2(Y2)+m2(Y3)]+m1(Y2)*[m2(Y1)+m2(Y3)+m1(Y3)*[m2(Y1)+m2(Y2)]=0.99。1-K=0.01,按规则继续融合得,m(Y1)=0,m(Y2)=1,m(Y3)=0。融合结果很明显出现了矛盾,本来几率很大的Y1和Y2可能性却变成了0,概率很小的Y2却变成了1。改进DS理论中,引进证据相容度[15]的概念,mj(uk)、mj(uk)关于uk的相容度系数: R.,(uk)=八,jk (2),[m>k)+m(uk)]/2
由证据间的两两相容系数组合成相容矩阵:
R1,1R1,2…R1,n
RR•…R
丄、2,1r2,2 R2,n
Rn,1Rn,2…Rn,n
由相容系数定义,可知该矩阵为对角线元素为1的对称阵。此矩阵说明的是两条证据间的相互支持程度,支持度越高,可信度越高。绝对相容度为nS(uk):j=1,i那么理想相容度为n-1,可信度则为B(〜)=, n-1⑷
这样,在进行DS证据融合之前乘以可信度,也即可信度作为基本概率赋值的权重,然后依据证据融合规则重新进行计算。
3三角模糊数
3.1三角模糊数定义
对于具有模糊特征的信息评价,自然要选择具有模糊描述的语言,比如文字中的程度描述词,一般高、略高、很低、极低,而这些词语是不能作为信息系统的准确描述的,因为它们不能给人具体直观的感知,所以对这些不确定与不清楚的描述,必须要选择一种可以准确量化的工具,也即描述特征的三角模糊数(x0,x1,x2),其中x0表示特征描述值的下界,x1表示特征的最大可能取值,x2表示特征描述值的上界。
3.2三角模糊数距离
定义两个三角模糊数:(x0,x1,x2)、(y0,y1,y2),则两个模糊数的距离为、1/2d=]7[(y。-x0)2+(Y1-x1)2+(y2-x2)2]l
4基于改进DS的双重模糊数
这里把安全评估过程中各种组成部分分别确定为一种角色,分别如下:
专家群:由多个专家个体构成,设为Ex={Ex1,Ex2,EX3,…,Exk};资产集合:M={m1,m2,m3,m4,…,mt};威胁集合:Th={th1,th2,th3,th4,…,tn};脆弱元集合:P={p1,p2,p3,p4,…,ps}。其中,k,t,n,s取值为1,2,3……
4.1模糊评价相关矩阵
4.1.1矩阵意义
安全风险发生的损失矩阵:Y[y‘xt,风险可能性矩阵:Z[zy]^。其中y,j为第1种脆弱元对第j种资产的造成影响的大小,损失大小取值范围0-100,zy为第i种威胁利用第j种脆弱元造成损失的可能性大小,可能性大小取值区间0〜1,Y、Z均由专家的等级评价项构成。专家对可能性和损失的评价结果都划分为很低、低、稍低、中等、稍高、高和很高7个等级。
4.1.2矩阵来源
之前的文献只是考虑到了不同专家对信息安全系统的倾向和评价,而忽略了系统处在不同时间内的不同表现会导致专家本身判断的不确定性,比如专家对系统处于t1-t2时间段内的表现比较满意而给予安全性很高的评价,然而当处于时间段t2-t3内时,系统表现不佳,专家只能给予表现一般的评价,那么系统到底属于哪一级别呢?专家也不确定,这里采用改进的DS证据推理理论解决此问题,用DS理论所得的结果作为每一等级的权重。
损失矩阵Z[zy]nxs的元素的取值为:
ZH=ailZH|Ex1+^ijZij\Ex2+•••+anZn\Exk(i=1,2,…,n;j=1,2,…,s) (6)
可能性矩阵Z[Zy;Us的元素的取值为:
y>j=ayyyIExi+a,jy,j|Ex2+•••+U(i=1,2,…,s;j=1,2,…,t) (7)这里由于专家地位相等,故取《ij为1/k。
4.2风险值计算
对于信息安全由多种因素影响,这里采用模糊综合评判法来计算风险值。模糊综合评判法是一种有效多因素决策方法,利用以上步骤中得到的矩阵进行风险值计算,设风险值为R,贝IJ:R=h.L=Z[&]脚07[yjL (8)其中0表示模糊数乘法。
4.3基于改进DS的双重模糊评估算法
作为不确定性特征的一种表现形式,DS证据推理为决策不确定性信息提出了强有力的工具,本文证据推理方法将被用来测评信息安全中的不确定因素,并利用它与模糊综合评价方法的结合完成双重模糊信息安全的评估决策。具体步骤如下:
(1)确定信息安全系统的组成;
(2)利用三角模糊数确定专家评判信息安全系统元素性质的量化标准;
(3) 利用改进DS理论对专家态度进行筛选校准;
(4) 基于专家态度的损失矩阵与可能性矩阵确定,并根据两矩阵进行风险值计算;
(5)威胁排序,规定最佳三角数,计算三角模糊数与最佳三角数(g)的距离,得到的值作为评估值,评估值越大,证明与最佳值距离越远,与期望效果相差越大,证明其表现越差。
5实验分析5.1DS改进算法验证
5.1.1 DS理论算法有效性证明
假设专家一的态度集中在B、C、©和B、A、©,其中@表示不确定性,也就是A~G全级,®取所有取值的平均值(0.4,0.5,0.8),这里借鉴层次
分析法中的认知判断矩阵,得到专家的评价倾向矩阵如表1
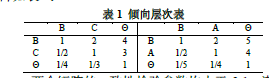
两个矩阵的一致性检 险验参数均小于 0.1,满足一致性条件,用评价矩阵的最大特征值对应的特征向量归一化后,作为每个等级的基本概率赋值,结果为m1(B)=0.5584,m1(C)=0.3196,m1(©)=0.1220;m2(B)=0.5695,m2(A)=0.3331,m2(©)=0.0974。按公式(3),分别的各个证据的绝对相容度为:S1(B)=S1(C)=S1(©)=S2(B)=S2(A)=S2(©)=1,即各证据的比重则可按其基本概率赋值来决定。据公式(1),m1、m2融合得m(B)=0.7535,m(C)=0.0917,m(A)=0.1197,m(©)=0.0350。得评价分值为:S=B*m(B)+C*m(C)+A*m(A)+0*m(0)(9)S=0.7535(0.7,0.9,1)+0.0917(0.5,0.7,0.9)+0.1197(0.9,1,1)+0.0350(0.4,0.5,0.8)=(0.695,0.880,0.984),结果与等级B的结果约等,因为两个评估倾向都倾向于B,其值自然倾向于B的取值,验证了算法的可行性。
5.1.2 DS理论算法必要性证明
如果将表1中的矩阵2替换为表2:
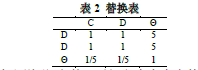
意义说明:在某一时间段内专家在等级C和D之间摇摆不定,无法选择,按照2.1中步骤计算得:m2(C)=0.4546,m2(D)=0.4546,m2(©)=0.0908。进而得:m(B)=0.1563,m(C)=0.6831,m(D)=0.1339,m(©)=0.0267。按公式(9)最终结果为(0.5018,0.6991,0.8862),近似等于C等级的取值,但是如果按第一种决策方法,专家可能会选择B等级,因为B等级比C等级占优;如果按第二种方式选择,C等级和D等级有相同地位,所以也有很大的可能选择D等级,这样也与最合适答案失之交臂。单从推理角度来讲,C在第一、二两种选择中虽然不是唯一的也不是最优的,但是却只有C等级是同时出现在这两个决策里的,而且在第二个决策方式中C是占优的,这样来看选C等级也是在情理之中的。
5.2算法验证
5.2.1双重模糊算法验证
这里邀请三位专家对系统进行评价,资产集合M={m1,m2},其中m1表示无形资产(数据资料等),m2表示有形资产(硬件设备);威胁集合Th={th1,th2},其中th1表示非法访问(对数据集或者对硬件设备恶意浏览、使用或篡改),th2表示资产丢失;脆弱元集合P={p1,p2,p3},其中p1表示物理设施保护欠缺,p2表示(0.9,1,1)资产控制不严格,p3表示访问控制漏洞。原始七个等级分别标注为A、B、C、D、E、F、G,以及三角模糊数对应关系如表3:
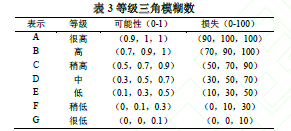
经过2.2的DS判断,得专家态度如表4、5所示:按公式(6)(7)计算得两矩阵如下:
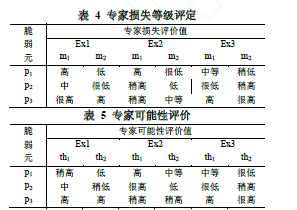
(56.67,76.67,90)(3.33,13.33,30)(26.67.40.56.67)(20,33.33,50)(70.86.67.96.67)(63.33,80,90)_(0.5,0.7,0.87)(0.4,0.5,0.6)(0.63,0.83,0.96)(0.13,0.27,0.43)(0.2,0.37,0.57)(0.7,0.87,0.97)
据公式(8)得风险矩阵"(83.10,145.61,205.11)(61.70,110.90,164.77)
将矩阵R按列归一化得:"(0.41,0.71,1)(0.30,0.54,0.80)
正常期望威胁值和损失值都为g1(0,0,0),最不理想取值为g2(1,1,1),据公式(5),得d1(r1,g1)=1.46,d2(rng2)=0.81,d《r2,g1)=1.24,d2(r2,g2)=0.95,可得威胁th1和威胁th2与期望值的距离比重为C=d1/(d1+d2),距离越大,证明效果越差。C1=1.46/(1.46+0.81)=0.64,C2=1.24/(1.24+0.95)=0.57.C1>C2,故可得非法访问严重程度大于资产丢失。这样,管理者便可以清楚,更加注意非法访问隐患。
5.2.2专家评估值发生少量变动时的对比
利用matlab对本文算法进行实现。
对比1,为了做简单对比,此处仅选择Ex(p2,m2)和Ex1(p2,th2)处的等级都变为高,得到C1=0.64,C2=0.63。由结果可知,非法访问的评估值并没有因为等级的变化而改变太多,但是资产丢失的威胁程度因等级变高而提高了,所以等级评价的不准确所造成的影响是不确定的。
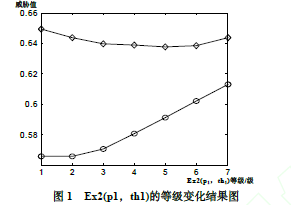
对比2,当只有专家二对脆弱元一所造成的可能性不确定,即Ex2(p1,th1)的等级取值由A-G变化时,得到C1、C2的仿真结果如图1,其中菱形块代表C1,圆圈代表C2,横坐标1-7代表等级取值A-G,知C1、C2会随Ex1(p1,th1)的变化而变化,但总体C1威胁程度一直大于C2。
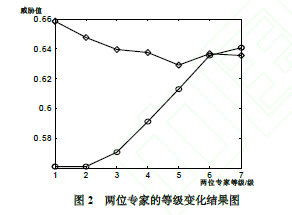
对比3,当两位专家对脆弱元一的可能性不确定,即Ex1(p1,th。、Ex2(p1,th1)的等级取值由A-G变化时,得到C1、C2的仿真结果如图2,可见C1、C2的取值大小已发生部分转换,这时威胁程度发生变化,管理员需重新规范管理先后;
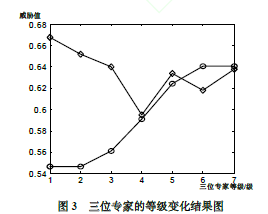
对比4,当三位专家对脆弱元一的可能性不确定,即Ex1(p1,th〗)、Ex2(p1,th〗)、Ex3(p1,th。的等级取值由A-G变化时,得到C1、C2的仿真结果如图3,可见C1、C2的取值大小已发生越来越多的转换,这时威胁程度受影响变动更大;
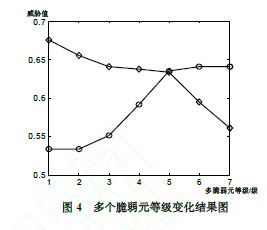
对比5,在对比4的基础上,如果再加上一位专家关于脆弱元2的可能性取值的不确定,得到的仿真结果如图4,等级的不确定性越多,对C1、C2的影响程度越严重。这些范例足以证明第一步中DS决定等级的重要性和必要性,这里仅仅改变的是两个脆弱元,如果是多个,后果将不可预知。
5.2.3和其他评估模型的比较
邀请30位信息安全领域专家对所在学校的学生信息管理系统信息安全做评估,采用三种评估模式进行评估,本文提出的基于改进DS理论和三角模糊数的双重模糊评估算法与单一DS理论和单一综合模糊评判比较,得到专家评估结果数据与实际信息系统表现比较得表:
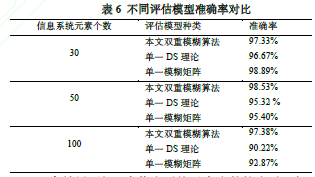
由结果可知,当信息系统元素个数较小时,本文的双重模糊与其他两种单一模糊没有太大差别,都可以较为准确地评估出最后结果,而随着评估元素个数的增加,在专家对较多的元素比重选择不明确的情况下就造成了误判,致使准确率下降,但是本文提出的基于改进DS和三角模糊数的双重模糊评估则可以将这种不确定因素量化均衡,从而得到相对更加准确的结果。
6结束语
本文在分析了现有信息安全评估方法的基础上,提出了利用DS证据推理和三角模糊数的双重模糊评估,相比其他仅有一次模糊评估的算法更有说服力,对不确定性的敏感度也更高。这里仅仅是做了个别方向的评估,对于复杂的信息系统,这些是远远不够的,尤其是云计算的出现,大数据的应用,使得问题更加复杂,下一步的目标就是如何将这些方法适应于现代新技术。
