数学知识向数学教学知识转化的个案研究 ——基

　　一、问题的提出

　　新一轮数学课程改革对教师数学教学知识提出了许多新的要求：“数学教学活动必须建立在学生的认知发展水平和己有的知识经验基础之上。教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者。

　　在这样的背景下，教师数学教学知识的发展显得尤为重要。当我们把目光投射到数学教师数学教学知识发展的己有研究时，由于数学教学知识概念本身的抽象性和内涵的广泛性，以及其发展机制的不确定性，使得无论是职前还是职后领域都很少有切实可行的发展办法。基于我国数学教师进行过长期数学知识的专门学习，具有较为扎实的数学知识这一优势，笔者认为有必要以美国学者舒尔曼(Shutnan)的学科知识向学科教学知识转化的理论为分析框架，采用个案研究的方法，在专家与新手教师知识转化外在行为的差异比较的基础上，从外显的角度来考察教师数学知识向数学教学知识转化这一内隐的过程。

　　二、初中数学教师知识转化的整体分析框架

　　舒尔曼将学科知识向学科教学知识转化的过程分为理解、表征、适应三个环节。其中，理解指的是教师对某一数学知识的认知情况，可以从理解的深度、广度和贯通度等角度进行深入的考察；表征主要是指教学中教师对数学知识的一种外在呈现和表达，是教师对该知识的内在认识的一种外部表现；适应主要指的是教师在教学中对表征的运用是否适应学生的状况，是否有利于对该数学知识的本质的反映。

　　本研究将知识转化的过程作进一步的细化：将表征又进一步细分为教学任务的运用、表征的方式、表征的目的以及对教科书中规定的任务水平的调整等四个方面；将适应分为对学生和对数学知识两方面的适应性，即对学生状况的关注主要体现在教师对学生学习某数学知识困难的预见，对数学知识的本质的关注主要体现在表征的形式与该数学知识关系的紧密程度上。为此，本研究以此框架来分析教师的知识转化水平。

　　三、研究设计与过程

　　1.个案的选取

　　该研究的个案是在某市某农村中学的初中数学教师中进行选取的。一名是新手教师，用N来表示，一名是专家型教师，用E来表示。其中，新手教师选取相对来说比较容易，只需要满足：教龄为1~5年的任课教师，专家型教师的选取对研究结论有着直接的影响，因此在选择上比较慎重，具体选取方式是在联合提名（通过校方、同事与学生的推荐，取其共同提名）的基础上，要求满足教龄在10年以上，具有高级以上的专业技术职称、市级或国家级骨干教师等条件，并结合课堂观察，综合运用多重标准最后确定下来。

　　2研究的工具

　　(1)制作概念图

　　概念图（coiceptnap)是由美国康奈尔（Conel)大学的诺瓦克（Ncvk)和高文（Gowin)基于奥苏贝尔(Ausube)的学习理论，在20世纪60年代开发的一种能形象表达命题网络中一系列概念含义及其关系的图解。12概念图作为一种研究工具，以图的形式来呈现思考的过程和知识的关联，概念图的一个显著特征是具有阶层性，在概念图中离中心概念位置越近的概念与中心概念的关系越密切，位置越远的概念与中心的关系越疏远。这便于对制作者的知识结构及组织情况的考查。概念图作为一种评价的工具被广泛地应用于对学生认知结构的研宄，但最近逐渐发展为对教师知识的评价上，有研宄表明概念图是评价教师知识比较可靠的工具（SahHogiNaicyQRodeNacyTeman&JulianWeisgas，s2007)本研宄采用让初中数学教师绘制某一具体数学知识概念图的方式，对概念图进行结构分析（stncturalaaysis)和内容分析（contentailSss以考查他们对数学知识理解的程度，分析该理解在进行数学知识向数学教学知识的转化的作用。在知识转化过程中，教师对数学知识的理解主要是采用概念图的方式来评价，其结构分析的评价指标如表1所示。

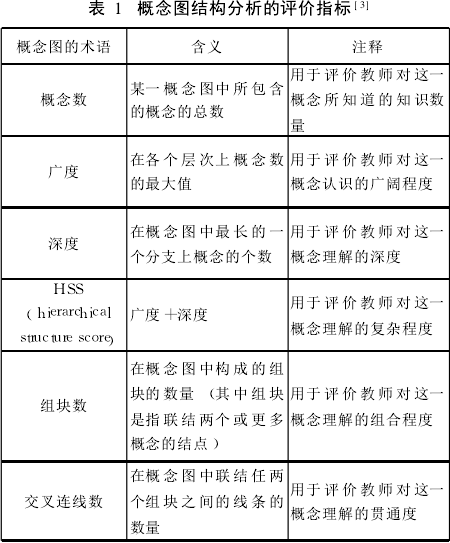
　　(2)课堂教学录像的编码

　　我们把在课堂听课观察到的教师的知识转化过程的外在表现分为对理解的表征和表征的适应性等两个方面，统称为教学表征行为，这是教师知识转化的外在体现，它包括：表征的形式、表征的目的、使用的教学任务的类型以及对教科书中任务的调整、表征对学生的适应性以及表征对数学知识本质的适应性等六个维度。基于录像分析技术，使复杂的课堂信息回放、重复观看教学表征行为，可以对课堂中教师的教学表征行为进行编码，整合定性和定量的分析。

　　编码是TMSS研宄中大量发展起来的分析方法，对于大规模的研宄来说必不可少，包括编码的维度、开发编码的具体程序、建立多级的编码系统等。编码的实质是不断地分类，分类的结果则重在有利于对研宄的问题可以建立一个统一的判断标准和尽可能反映比较研宄中教学现象的差异，有很多关于数学教学的比较研宄都采用了此方法。本研宄中对教师教学表征行为的编码方法主要由表征及适应两个维度组成，前者包括教学任务类型（分为记忆型解释型和探宄型)表征方式（分为单一表征多元表征关联表征R转化拓展表征T)表征目的（分为解释验证和防误)对教科书任务的调整（分为提高保持和降低)等四个方面；后者包括关注情况（由关注学生的情况XQ和关注数学的本质两部分组成）和选取的情况（分为无力选取费力选取FL顺畅选取和自动化选取)两方面。在编码信度上，采用两人同时编码的形式来检验编码的一致性。

　　四、研究的发现

　　针对新手与专家型教师对同一单元“图形的平移与旋转”的知识转化情况进行了横向的比较分析。“图形的平移与旋转”单元是数学课程改革以后新增加的内容，可以以小见大地探求课程改革后新增内容的课堂实施的情况。经过近一个月的课堂观察，对教师N与专教师E的同一主题的授课进行了录像分析，重点编码分析了12节新授课(每位教师各6节）得出如下的结论：

　　1.在数学知识理解上的差异

　　通过新手教师与专家型教师所制作的关于“图形的平移与旋转”的概念图的比较，我们可以从结构分析和内容分析两方面，得出新手教师与专家型教师在数学知识理解上的差异。运用概念图评价指标，对两位教师所作的概念图进行了结构比较分析，结果为：新手教师和专家型教师在概念数、广度、深度、HSS组块数和交叉边线数上分别为9和226和93和89和173和72和4从数据比较中可以看出，专家型教师E的概念图结构比新手教师N的概念图结构更加复杂，无论是广度、深度，还是知识的贯通度（交叉连线数）的数据都是教师E的要大于教师N的，这说明教师与教师相比，对“图形的平移与旋转”知识的理解更为深刻。

　　为了更为深入地分析两位教师在“图形的平移与旋转”这一知识点上理解的差异，我们除了对概念图进行了以上的结构分析，还进行了概念图的内容比较，结果发现教师N和教师E在本章内容的概念数、涉及其它章节内容的概念数、涉及数学之外的内容的概念数等三个维度方面的数据分别为9和140和7、0和2即教师N对“图形的平移与旋转”的理解仅关注该知识本身，涉及的都是本单元的内容，很少或几乎不考虑本单元内容与其它相关单元内容之间的关系，以及与学生的生活实际的联系，而教师E相比之下更加关注所教知识的前后左右间的联系，关注学生己有的知识与经验。

　　通过对教师E与教师N所作的关于“图形的平移与旋转”的概念图的结构与内容的比较，可以看出，教师E对此知识的理解更为深刻、知识的组织结构更加系统、知识之间的联系更加的广泛。

　　2.在教学表征上的差异

　　(1)表征的目的

　　在表征的目的上，该单元的教学中，教师E与教师N在注重解释的同时（分别为46.2%和588%)也体现出较大的差异：教师E倾向于防误（25.(%)，通过表征的运用，防止学生对数学知识的常犯错误的产生，而教师N倾向于验证（5.9%)表征的目的集中于对数学知识的验证。

　　(2)教学任务的运用

　　在所使用的教学任务上，两位老师在课堂中采用的教学任务的类型上表现出不同的特点。教师E与教师N相比，更倾向于使用探宄型或解释型的教学任务，在这单元所使用的所有教学任务中有90%多的任务都是这两种类型的；其目的在于帮助学生对知识的理解，在数学知识向数学教学知识进行转化时，主要设置的是探究型的教学任务，让学生参与到教学活动中，获得活动的经验，建构对知识的理解。而教师N在所有的教学任务中三种类型的教学任务使用比较平均（记忆型、解释型和探究型分别为30.8%、38_5%和307%)其记忆型任务和解释型的设置方面明显地高于专家型教师E说明教师N在知识转化时，所设置的教学任务主要是为了帮助学生加深对知识的记忆，或是向学生提供知识的合理的解释，以期能帮助学生在理解的基础上对知识进行记忆。

　　(3)表征的方式

　　在表征形式上，教师N和教师E在“图形的平移与旋转”这一个单元中所使用的语言表征、图像表征、符号表征、具体操作表征和情景表征等各种呈现表征方式的出现频率分别为41.2%和20.5%、29.4%和256%、11.軏和7.7%5制和20.5%、11.8%和25.6%

　　数据表明，该单元的教学中，教师E与教师N在各表征方式上的差异主要体现在情景表征、具体操作表征和语言表征这三个方面。教师E与教师N相比，更趋向于使用情景表征和具体操作表征来进行知识的呈现，让学生通过动手操作的活动和自身熟悉的情景来体验、感悟和理解活动与情景中所蕴含的数学知识，并且往往采用多种表征来呈现某一教学任务；而教师N在数学知识的呈现上，往往采用单一的方式进行某一教学任务的呈现，而使用比较多的是直接的语言表征的方式，主要进行知识（定义、公式、法则、定理等）的讲解（占90%)以期能通过对这些知识的解释使学生记忆和理解它们，较少使用语言表征中的另一种方式：数学交流。与此相反，虽然教师E使用的语言表征的方式不多，但大部分是集中在教师与学生的数学交流、丰富深刻地讨论数学和能激发学生高水平思考的问题上（占80%)

　　(4)对教科书任务的调整

　　在对教科书任务的调整方面，教师N与教师E表现出很大的差异：他们在提高、保持和降低三个维度上的频数分别为0%和38_5%23.1%和385%、769%和15.4%。教师N表面上趋向于使用教科书上的任务，但实际上是“形似而神非”，大部分表现为对教科书中任务的异化，使得许多高认知水平的任务降低为记忆型等低认知水平的任务；而教师E虽然不一定是用教科书中的任务进行教学，但能有效地保持教科书中所设计的教学任务的水平或能根据学生的认知水平提高教科书中任务的水平。

　　(5)表征的适应

　　在表征的适应性方面，两位教师在“图形的平移与旋转”单元的课堂教学中分别表现出不同的特征。我们通过对课堂实录的编码分析，运用简单统计的方法，对教师N与教师E对表征的适应性进行了分析，发现教师N和教师E在表征对学生情况的关注次数和表征对数学本质的关注次数方面，分别是5和1510和12数据表明：教师E与教师N相比更为关注表征对学生的适应性，教师E的关注量是教师N的3倍；而对数学本质的关注，教师E略高于教师N并且我们对教师E对学生的关注进行了细致分析，发现他更多的是关心学生学习某一数学知识的困难，关注学生的认知水平。由此可以推测出，造成这种差异的原因可能与教师对学生学习困难的预测能力有关。为此，笔者对两位教师就这个单元的内容进行了预测能力的检验，过程与结论如下。

　　首先，我们选择了这个单元的6个问题对教师和学生分别进行了测试，通过教师与学生对这6个问题的难度估计的一致性程度，以确定该教师能否有效地预见本单元中学生学习的困难；再用同样的测试问卷对教师N和E进行困难预测能力的测试，其结果如表2所示：

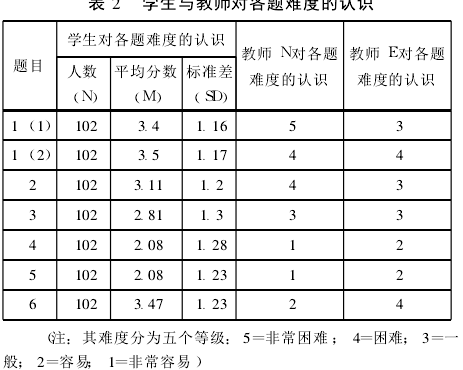
　　其次，再把以上数据综合在一个图中，以此来较为鲜明地反映两位教师对学生学习困难的预测能力的差异。

　　从数据综合图可以看出，教师E的难度预见曲线基本与学生对各题目难度的认识相吻合，说明该教师能较为准确地预见题目的难度，具有较强的预见学生学习困难的能力；而教师N对题目难度的预见，要么高于学生对题目难度的认识，要么低于学生对题目的平均认识水平，说明该教师不能较为准确地预见题目难度，对学生学习困难的预见能力不强，往往表现为高估或低估学生的水平。由此可以解释为什么教师E所应用的表征更适应于学生。