浅谈数学教学中的数形结合思想

　　随着教学改革的不断深入，针对数学中如何渗透数学思想方法，在教学界掀起了一个讨论、研究的热潮。数学思想是分析、处理和解决数学问题的根本想法，是对数学规律的理解认识，掌握这些思想可以为进一步学习高等数学打下良好的基础。关于数学思想归纳起来大致有如下几种:方程思想、分类思想、数形结合思想、整体思想、函数思想、化归思想等。在数学教学中数形结合思想是应用十分广泛的一种数学思想，在教学中注重数形结合思想的培养，是提高学生数学素质的一个重要途径。

　　数形结合是运用形和数的相互关系来解决数学问题的思想方法。“形”与“数”是数学中最基本的2个概念，是直观与抽象在数学中的体现，二者的有机结合，是数学魅力之所在。通过形数结合，可将抽象的数学语言与直观的图形相结合，把数量关系转化为图形的性质来研究，思路与方法便在图形中直观地显示出来。以形助教，可显现直观，简化解答，往往起到事半功倍的效果。数形结合的思想方法在中学数学中应用十分广泛。在数学中如何将数式的准确刻划同几何图形的直观描述有机地结合起来显得尤为重要，它对发展学生的创造性思维、完善学生的思维品质起着重要作用。

　　1数形结合思想的内涵及地位

　　由于数形结合思想通常是使复杂问题简单化，一般问题特殊化，抽象问题具体化，化复杂为简单，化新知为旧知，化未知为己知，最终使问题得以解决。而任何一个数学问题的提出都是待解决的，在解决的过程当中，经常要用到上述处理方法，这显示数形结合思想在众多数学思想中占据着十分重要的地位。数形结合作为一种常见的数学方法，沟通了代数、三角与几何的内在联系，借助图形直观地研究数学问题，不仅可以加深对数量关系的理解，而且还可以简化运算过程;借助数式关系，还可以简明地抽象出一些几何问题的证明思路。因此，数形结合，常常能为合理解决有关问题提供一条便于接受的思路，它有助于探求问题途径、避繁就简、巧妙地得出结论，是提高解决问题能力的一种重要手段。

　　在数学教学中，数形结合思想的确立，对培养学生的分析综合能力、空间观察能力、解决实际问题的能力都起着很重要的作用；数形结合思想的形成也是培养学生辩证唯物主义观点中“相互转化观点”的重要途径。因此，数形结合思想是在数学教学中要求学生确立的最基本的数学思想之一。

　　2数形结合思想在数学教学中的具体表现21利用图形进行数形结合教学

　　在数学中有些不等式在求解时方法甚繁，而且有可能在转化时考虑不周反而会与题意不符，造成多解或失根。这就要求老师在教学时要注意树立数形结合的思想，要按照把复杂问题化简单的原则培养学生的视图观察能力，以培养其空间概念。

　　22结合几何解题进行数形结合教学

　　有些较难的几何证明题，学生看到后往往眼花缭乱，无从下手，此时若借助于代数的方法，可较快地寻求到解题途径。

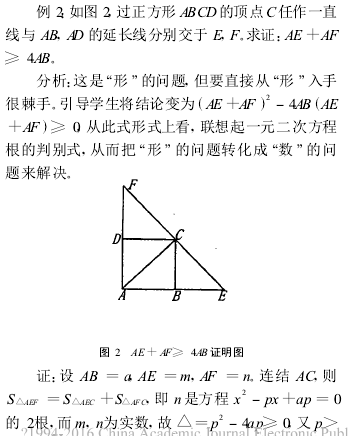
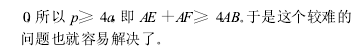
　　23把握好数形结合的尺度

　　“数”与“形”是数学研究的两类基本对象，也是矛盾的双方，两者相互依存，既对立又统一。在运用数形结合的思想和方法时，如果片面夸大或抑制“数”或“形”中的一方，常常会使我们的解题陷入困境或导致错误。

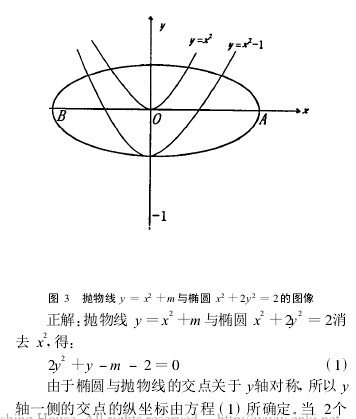
　　总之，正确理解“数”与“形”的相对性，使之有机地结合起来，掌握好度，对顺利解题很有好处。经验告诉我们，当寻找解题思路发生困难时，不妨用数形结合的观点去探索；当解题过程中的复杂运算使人望而生畏时，不妨用数形结合的观点去开辟新径。当然，要灵活运用数形结合的思想方法，就要熟悉某些问题的图形背景，熟悉有关数学式中各参数的几何意义，建立结合图形思考问题的习惯，在学习中不断摸索，积累经验，加深和加强对数形结合思想方法的理解和运用。

　　3数形结合思想的培养和发展

　　通过一些例题的讲解使学生首先对数形结合这一重要数学思想方法有一个初步认识，让学生们体会到其实质是将抽象的数学语言与直观图形结合起来，使抽象思维和形象思维结合起来，实现抽象概念与具体形象的联系和转化，化难为易，化抽象为直观。通过一些刻意准备和具有代表意义的练习使学生们深刻认识到数形结合的妙处。使之看到有的代数问题，通过把数量关系转化为图形性质问题讨论，或者有的几何问题把图形的性质问题转化为数量关系问题来研究，相应问题就会化抽象为直观，化难为易，一些原来看似很难的问题就会迎刃而解，使问题简捷地得以解决。这样学生学习兴趣上来了，积极性也提高了，这时老师可再准备一些习题让学生们有意识地训练，并在日后的教学当中教师要尽量发掘数与形的本质联系，促使学生善于运用数形结合的思想方法去分析问题，解决问题，并要及时地启发学生注意数形结合与转换，让其对数形结合思想达到能够自觉运用的程度，从而提高学生的数学能力。

　　通过以上几个方面的探讨，我们己领略到数形结合在解题中的美妙所在了。数形结合思想在数学解题中运用很广泛，它蕴含在课本的字里行间之中，渗透在学习新知识和运用知识解决问题的过程之中。这就要求教师平常应加强数形结合的教学，强化化数为形，以形表数的意识，这样不但在解题时，可化难为易，简捷地得出结论，还可以发挥学生的想象力，将原有认识结构进一步提高，是深化思维的一种有效训练，使学生既学到了知识，又提高了能力，同时也増添了学习兴趣，使学习变得轻松愉快。

　                            　    张宏良

                        　　(衡水财贸学校微机室，河北衡水053000)